Regression Analysis in Python

Usman Malik
Man's hands working on business reports at the office.

Regression analysis is one of the most fundamental tasks in data-oriented industries. In simple words, it involves finding a relationship between independent and dependent variables (attributes) in a given dataset.

Consider the example of a house price prediction problem—given the size and number of bedrooms, we want to predict the price of a house. This is a simple regression problem where the size of the house and the number of bedrooms are the independent variables and the price of the house is the dependent variable.

A myriad of other financial tasks involve regression analysis. For instance, if you want to find the probability that a customer will repay a loan, you can perform regression analysis on the data of past customers who borrowed loans. Estimating the value of a particular financial asset that depends on a variety of features also involves regression analysis.

In this article, we’ll study a type of regression where two or more variables are linearly related. This is known as linear regression.

Linear Regression: Mathematical Intuition

Mathematically, linear regression can be represented as follows:

$$Y = w_1x_1 + w_2x_2 + w_3x_3 + … w_nx_n$$

Here, Y is the dependent variable, while x1, x2, x3, …, xn are the independent variables. Additionally, the coefficients w1, w2, w3, …, wn represent the weight (or contribution) of each independent variable in determining the value of the dependent variable (Y).

In regression analysis, independent variables are also known as explanatory variables because they help explain the trends (if any) that we see in the dependent variable. The dependent variable is also known as the response variable because it responds to changes in the explanatory variables.

We change the values of the independent variables as they appear in our dataset; the only cannot thing we can update is their weights. Said differently, we adjust the weights to change how much emphasis we place on any particular variable’s contribution to the value of Y.

In regression analysis, the values for the weights are determined in such a way that the difference between the predicted value for Y (per the equation above) and the actual value for Y (per the dataset—the actual house prices) is minimized.

Performing Regression Analysis with Python

The Python programming language comes with a variety of tools that can be used for regression analysis. Python’s scikit-learn library is one such tool. This library provides a number of functions to perform machine learning and data science tasks, including regression analysis.

The Dataset: King County Housing

In this article, we’ll see how we can use Python for regression analysis. We’ll predict the price of a house based on different attributes, such as size, condition, grade (as assigned by the local municipality), and year built.

The dataset that we’re going to use for this problem can be downloaded from this kaggle link. This dataset contains house sale prices for King County, Washington and includes homes sold between May 2014 and May 2015. I’ve renamed the dataset to housing_data.csv; you can give it any name.

Note: All the code in this article is executed using the Spyder IDE for Python.

Step 1: Import the Required Libraries

We need to import the pandas, numpy, and matplotlib libraries in order to load and analyze our dataset. Execute the following script to do so:

import pandas as pd  
import numpy as np  
import matplotlib.pyplot as plt

The default figure size created using matplotlib is 6 x 4 inches in the Spyder editor for Python development. However, for a clear understanding and better analysis, let’s increase the default size of the plots to 10 x 8. The following code does that: 

fig_size = plt.rcParams["figure.figsize"]
fig_size[0] = 10
fig_size[1] = 8
plt.rcParams["figure.figsize"] = fig_size

Step 2: Load the Dataset

We’ll use the read_csv function of the pandas library to read our dataset into a DataFrame:

housing_data = pd.read_csv(r'E:\Datasets\housing_data.csv')

Step 3: Perform Exploratory Data Analysis

It’s always a good idea to look at any trends in our data before performing regression to gain some insight. Let’s first observe the shape of our dataset:

housing_data.shape

In the output, you should see (21613, 21), which means that our dataset contains 21613 rows and 21 columns.

In this article, we will perform regression analysis using only the following four features:

  • sqft_living — contains the size of the house in square feet.
  • yr_built — contains the year that the house was built.
  • condition — corresponds to the condition of the house.
  • Grade — the grade assigned to the house based on the King Count grading system.

Let’s filter out all the relevant features of our dataset and discard the rest (note that price is going to be the dependent variable):

housing_data = housing_data[['sqft_living', 'yr_built', 'condition','grade', 'price']]

Learn the world’s most popular data analysis language so you can mine through data faster and more effectively. No IT background needed.

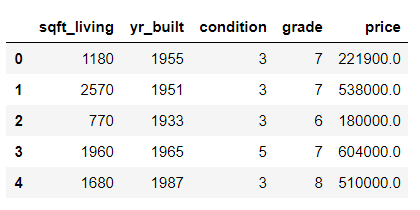
Now let’s see how our data actually looks. We can use the head function of the pandas DataFrame to do so; it returns the first five rows from the dataset.

housing_data.head()

In the output, you’ll see the first five rows of the data as shown below:

Table 1

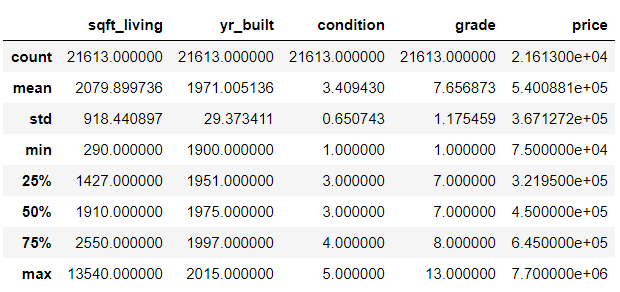
Similarly, to see the statistical details of the data, we can use the describe function:

housing_data.describe()

This returns the following information:

  • The number of values in each column.
  • The average (mean) of each column.
  • The standard deviation of each column.
  • The maximum and minimum values for each column.
  • The 25th, 50th, and 75th percentiles of the values in each column.

In the output, you should see something like this:

Table 2

Step 4: Visualizing the Data

Let’s see the relationship between the area of a house and its price. We can use the plotly.offline.plot function of the plotly library. To make plotly work with the pandas dataframe, we will use the cufflinks library. Remember, cufflinks library works with plotly library version 2.7.0. Execute the following script to connect the pandas library with the plotly library.

import cufflinks as cf
from plotly.offline import download_plotlyjs, init_notebook_mode, plot, iplot  
cf.go_offline()

Let’s now plot the relationship between the size of the house and its price:

housing_data.iplot(kind='scatter', x='sqft_living', y='price', mode='markers', color = '#5d3087',  layout = {
        'title' :'Size vs Price',
        'xaxis': {'title': 'Size', 'type': 'log'},
        'yaxis': {'title': "Price"}
    } )

You should see the following plot in the output:

You can see that there is a slight positive correlation between the size and price of a house. However, after roughly 8000 square feet, the effect of the size on the house price starts diminishing.

Correlation simply refers to the relationship between two variables, where an increase or decrease in the value of one variable causes an increase or decrease in the value of the other variable. In a positive correlation, the values of both the correlated variables move in the same direction. In a negative correlation, an increase in the value of one variable causes a decrease in the value of other, and vice versa.

Let’s now plot the relationship between grade and price:

housing_data.iplot(kind='scatter', x='grade', y='price', mode='markers', color = '#5d3087',  layout = {
        'title' :'grade vs Price',
        'xaxis': {'title': 'grade', 'type': 'log'},
        'yaxis': {'title': "Price"}
    } )

Here is the output of the above script:

You can clearly see that there’s a positive correlation between the grade and price of a house. In other words, houses with higher grades tend to have higher prices compared to houses with lower grades.

Finally, let’s plot the relationship between year built and price:

housing_data.iplot(kind='scatter', x='yr_built', y='price', mode='markers', color = '#5d3087',  layout = {
        'title' :'Year vs Price',
        'xaxis': {'title': 'Year', 'type': 'log'},
        'yaxis': {'title': "Price"}
    } )

The output looks like this:

You can see that the relationship between the price of a house and the year in which it was built is purely random. The relationship between two or more variables is random when no correlation, either positive or negative, is observed between them.

Step 5: Creating a Linear Regression Model

Now that we have a general idea of the trends in our dataset, let’s see if our regression model confirms our observations.

To perform regression using Python’s scikit-learn library, we need to divide our dataset into features and their corresponding predictions. By convention, the feature set is represented with the variable X, and predictions are stored in the variable y. However, you can use any variable names for these.

Let’s divide our dataset into features and predictions:

X = housing_data[['sqft_living', 'yr_built', 'condition','grade']] 
y = housing_data['price']

To evaluate the performance of our regression model, we’ll also divide our data into a training set and a test set. The training set contains data that will be used to train our regression model. In the training process, we’re basically finding a mathematical equation that minimizes the difference between the actual values of the dependent variable (price) and the values that we predict with our model (Y).

As a rule of thumb, a regression model should be trained on one part of the data and tested on another, known as the test set, that our model has not seen. This practice of dividing data into training and test sets ensures that our regression model is robust and can make good predictions on data that it has not encountered in the past.

Execute the following script to divide the data into a training set and test set:

from sklearn.model_selection import train_test_split  
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)

Here, the value of the test_size argument specifies the percent of dataset values that should be used for the test set. That is, a value of 0.25 means that our test set will consist of 25% of the actual data, while the training set will consist of the remaining 75%. You can use any value for test_size.

Next, we need to train our regression model. As explained earlier, training a regression model refers to finding a mathematical equation as described in the Mathematical Intuition section.

Python’s scikit-learn library contains the LinearRegression class for this purpose. To create a regression model based on the training data, we need to call the fit method of the LinearRegression class and pass in our features and predictions, as shown below:

from sklearn.linear_model import LinearRegression  
reg = LinearRegression()  
reg.fit(X_train, y_train)

Once our regression model is trained, we can extract the coefficients (the Ws) that our model found for each independent variable (feature). Execute the following script:

attributes_coefficients = pd.DataFrame(reg.coef_, X.columns, columns=['Coefficient'])  
attributes_coefficients

In the output, you should see the following values:

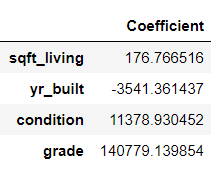
Table 3

According to to this model:

  • Each square-footage increase in area causes an increase of $176 in the price.
  • Each increase of one year in the year built causes a decrease of $3541 in the price.
  • Each one-unit increase in a house’s condition causes an increase of $11379 in its price.
  • Each one-unit increase in the grade of a house causes an increase of $140779 in its price.

With this information, we can now test the performance of our regression model on the test set:

y_pred = reg.predict(X_test)

comparison = pd.DataFrame({'Actual': y_test, 'Predicted': y_pred})  
comparison

Here’s a snippet of some of the comparisons between actual and predicted house prices:

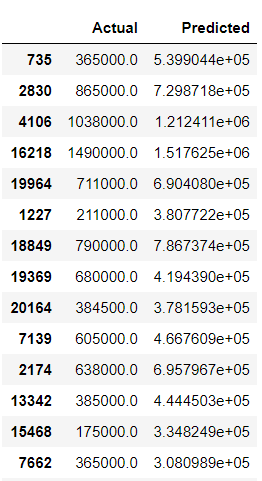
Table 4

You can see that our regression model has made some closes guesses regarding the prices—and, in some cases, is very far from the actual price.

Step 6: Testing the Linear Regression Model

Once you’ve trained your regression model, the next step is to evaluate its performance. This is very important—if your model isn’t good enough for predictions, there is no point in using it.

Learn the world’s most popular data analysis language so you can mine through data faster and more effectively. No IT background needed.

There are different metrics to evaluate the performance of a regression models. The root-mean-square error (RMSE), mean squared error (MSE), and mean absolute error (MAE°) are the most commonly used metrics.

The scikit-learn library contains built-in functions for calculating these values. Execute the following script to calculate each one, in order:

from sklearn import metrics  
print('MAE:', metrics.mean_absolute_error(y_test, y_pred))  
print('MSE:', metrics.mean_squared_error(y_test, y_pred))  
print('RMSE:', np.sqrt(metrics.mean_squared_error(y_test, y_pred)))

In the output, you should see the following results:

MAE: 150410.9696916637
MSE: 59028208836.96216
RMSE: 242957.21606275075

You can see that our value for the RMSE is quite large. As a rule of thumb, the RMSE should be less than 10 percent of the mean value of the predicted output.

As an exercise, try to add the remaining features of the dataset to the regression model, and see if you can achieve a lower value of RMSE.

Next Steps

Awesome! With Python’s scikit-learn library, we were able to develop a linear regression model to predict house prices based on different features in our dataset.

Regression is one of the most frequently performed tasks in finance. But as you can see, the process of performing regression analysis in Python is actually quite straightforward—it only takes a few lines of code.

Of course, this is just the beginning. In the real world, Python can be used to perform much more complex financial tasks, which we’ll look at in later articles. Stay tuned!

Looking to pursue a career in finance or data science? Consider learning Python to expand your professional toolkit and position yourself strategically in today’s competitive job market.

Usman Malik

I am a machine learning and data science enthusiast with over 5 years of industry experience. Currently, I am pursuing my Ph.D. in machine learning. Python is my passion, machine learning is my hobby and data science is my profession.

Related Posts:

Can Python Displace R for Data Science?

How to Create Python Heat Maps for Marketing Campaigns

Python Coding Best Practices and Style Guidelines