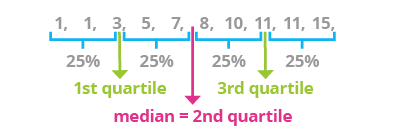Quartiles are the values that break down the dataset into quarters, or quartiles:
- The first quartile (Q1) is the point below which a quarter of the data lies. It is sometimes called the lower quartile.
- The second quartile (Q2) is the point below which half of the data lies. We already know this point by the name of median. It is also called the middle quartile.
- The third quartile (Q3) is the point below which three-quarters of the data lies. It is called the upper quartile.
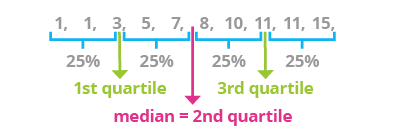
Let's calculate quartiles for the following set:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10
We already know how to calculate median (the middle quartile). In this case, the middle quartile is 5.5. Below this point, we have half the data \{1, 2, 3, 4, 5\}, and above this point, we have the other half, \{6, 7, 8, 9, 10\}. The median for the lower half of the data is 3; below this point, we have one-quarter of all the data, or half of the data for that subset. Thus, 3 is the lower quartile.
Let's now consider the second half of the set. The median of this set is 8, and this is also the upper quartile of the whole set.