The median is the middle value in a dataset. It separates the top and bottom ranges.

The general formula for the median depends on the number of observations(n) in the dataset:

• If n is odd, the median is the middle observation in an ordered list of dataset elements.
• If n is even, the median is the arithmetic mean of the middle two observations in an ordered list of dataset elements. In other words, we obtain the median for such a dataset by adding the two central values and dividing them by 2.

Let's use two sets of numbers to illustrate this concept.

Example 1:

The median of the first set is 3 because it is exactly in the center of the set. Two numbers are smaller thatn the median (1, 2), and two numbers are greater (4, 5).

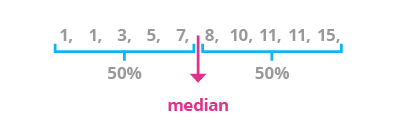
Example 2:

The median of this second set is 3.5. This is the arithmetic mean of the two middle values, 3 and 4. Exactly three numbers are smaller than 3.5 (1, 2, 3) and three numbers are greater (4, 5, 6).

Theoretically, any value from the interval between 3 and 4 can separate the set into two halves, but only the arithmetic mean is the true median because it is the exact midpoint of the data range.